- UID
- 24
- 积分
- 1778
- 帖子
- 99
- 主题
- 5
- 论坛币
- 3492
- 威望
- 8
- EP值
- 1453
- MP值
- 11
- 阅读权限
- 100
- 注册时间
- 2011-8-5
- 在线时间
- 137 小时
- 最后登录
- 2014-6-18
 
|
本帖最后由 showjim 于 2013-1-11 10:56 编辑
河亲,给我时间想想
打算写这次《AKB48 29th - 桜の花びら~前田敦子solo ver.》的制作经历吧,以后再写别的。
第一部分:均速贝塞尔曲线(Constant Bézier Curves)
1. 何为均速贝塞尔呢?
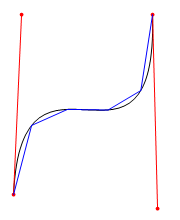
首先说说贝塞尔曲线,这里是WIKI: Bezier Curve。详细的不说,由于贝塞尔函数的变量是参数t,而且其与坐标x、y在除1阶贝塞尔的情况下都不是线性关系,如下图:

而均速贝塞尔曲线就是指曲线上的点均匀分布,如下图:
![5505HJ`E`6CK]CL_7ZXD%PV.jpg 5505HJ`E`6CK]CL_7ZXD%PV.jpg](static/image/common/none.gif)
2. 计算曲线长度
这个function主要是为了解决字体随贝塞尔曲线运动而做的。使用工具是NyuFX。
为了实现这个函数,我们首先要解决的是曲线长度的问题。但由于高阶贝塞尔的公式一般都比较复杂,所以我们可以用积分来得到想要的量。实现代码如下:- function curve_len(pct, spoint, tot_step)
- local sum = 0
- for i = 1, math.floor(pct * tot_step) do
- if i==1 then
- sum = 0
- else
- sum = sum + math.sqrt((spoint[i][1]-spoint[i-1][1])^2 + (spoint[i][2]-spoint[i-1][2])^2)
- end
- end
- return sum
- end
a) 分割曲线为5部分,误差较大

b) 分割曲线为8部分,误差较小
这个求长度的方法比较粗糙,但简单,在1080P以下的字幕分辨率下足够了。
3. 新的参量t'的计算
假设我们已经用N个点点描述了一条贝塞尔曲线,接下来就是如何实现点的均匀分布的问题
由于贝塞尔曲线上点的坐标轴在除一阶的情况下不与变量t是线性关系,所以为了实现均速取点,我们假设一个新的参量t',并认为t'满足以下关系:- t' = curve_len^-1[curve_len(1) * t]
由于直接计算任意n阶贝塞尔曲线公式的反函数比较困难,我们可以用牛顿法来取接近值,牛顿法可以参考维基百科:牛顿法
下面是Lua源码实现:- function constant_bezier(t1, spt, pts, tot_step, accuracy) --spt stands for the control points list, pts are the points on the curve, tot_step is the number of total step
- local len = curve_len(1, spt, tot_step) * t1
- local t2
- local t3
- local k
- repeat
- t2 = t1 - (curve_len(t1, spt, tot_step) - len)/DeriveSA(t1, pts)[1] --Newton's method
- t3 = t1
- if t2 <= 1 then
- t1 = t2
- else
- t1 = 1
- end
- until math.abs(t2 - t3) < accuracy
- local k = math.round(t3 * tot_step)
- return spt[k][1],spt[k][2]
- end
上一节代码中有个DeriveSA函数,这个我本意是用来计算导数的。实际上我换成了计算切向量与X轴的夹角。
任意阶贝塞尔函数的一阶导为:

式中,B代表Betnstein基函数,n代表总控制点数,i=0,1,2,…,n
而Betnstein基函数公式为:

Lua代码实现如下:- function D_bezier(pct, p)
- --Factorial
- function fac(n)
- local k = 1
- if n > 1 then
- for i=2, n do
- k = k * i
- end
- end
- return k
- end
- --Binomial coefficient
- function bin(i, n)
- return fac(n) / (fac(i) * fac(n-i))
- end
- --Bernstein polynom
- function bernstein(pct, i, n)
- return bin(i, n) * math.pow(pct,i) * math.pow((1 - pct), n - i)
- end
- local point = {0, 0}
- local n = table.maxn(p) - 1
- for i=1, n do
- local bern = bernstein(pct, i-1, n-1)
- point[1] = point[1] + (p[i+1][1] - p[i][1]) * bern * n
- point[2] = point[2] + (p[i+1][2] - p[i][2]) * bern * n
- end
- return point
- end
- function DeriveSA(pct, p)
- local D_pt = D_bezier(pct, p)
- local D_f = math.sqrt(D_pt[1]^2 + D_pt[2]^2)
- local theta = math.atan(D_pt[2]/D_pt[1])*180/math.pi
- return {D_f, theta}
- end
以上,第一部分完结。
参考:
1. Warping Text to a Bézier curves
2. 匀速贝塞尔曲线运动的实现 |
-
2
查看全部评分
-
|